Sifat –sifat eksponen atau bilangan pangkat diturunkan dari definisi bilangan pangkat. Sifat-sifat ini ditemukan pada perkalian bilangan pangkat dengan basis sama pangkat berbeda dan basis berbeda pangkat sama, pada pembagian bilangan pangkat dengan basis sama pangkat berbeda dan basis berbeda pangkat sama, dan pada perpangkatan bilangan berpangkat .
Agar lebih jelas, perhatikan contoh contoh soal eksponen dan jawabannya berikut
Contoh 1. Sederhanakan
jawab
Contoh 2. Sederhanakan
jawab
Sifat-1. Jika a bilangan real, m dan n bilangan bulat positif maka
bukti
Sifat-2. Jika a bilangan real, dan m bilangan bulat positif maka
bukti
Sifat-3. Jika a bilangan real dan a ≠ 0, m dan n bilangan bulat positif, maka
bukti
Sifat-4. Jika a dan b bilangan real dan b ≠ 0, m bilangan bulat positif, maka
bukti
Sifat-5. Jika a bilangan real, m dan n bilangan bulat positif maka
bukti
Agar lebih jelas, perhatikan contoh contoh soal eksponen dan jawabannya berikut
jawab
Contoh 2. Sederhanakan
jawab
Perhatikan bahwa dengan menganggap $q$ tidak 0 maka $q^{0}=1$ sehingga hasil akhir mempunyai pengali 1 dan boleh tidak dituliskan. Untuk memahami pangkat 0 silahkan lihat pangkat nol .
Contoh 3. Cari penyelesaian persamaan eksponen sederhana berikut
jawab:
a) Ubah 32 ke dalam perpangkatan dengan basis 2. Pangkat yang tepat untuk 2 yang menghasilkan 32 adalah 5.
Jadi penyelesaiannya adalah $x = 5$.
b) Ubah 27 ke dalam perpangkatan dengan basis 3. Pangkat yang tepat untuk 3 yang menghasilkan 27 adalah 3.
Jadi penyelesaiannya adalah $x = 2$.
Contoh 3. Cari penyelesaian persamaan eksponen sederhana berikut
jawab:
a) Ubah 32 ke dalam perpangkatan dengan basis 2. Pangkat yang tepat untuk 2 yang menghasilkan 32 adalah 5.
Jadi penyelesaiannya adalah $x = 5$.
b) Ubah 27 ke dalam perpangkatan dengan basis 3. Pangkat yang tepat untuk 3 yang menghasilkan 27 adalah 3.
Jadi penyelesaiannya adalah $x = 2$.




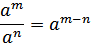















No comments:
Post a Comment